Ya
podemos disfrutar de un nuevo libro de Adrián Paenza. Este
ejemplar, publicado por Editorial Sudamericana, cuenta con el inconfundible
toque del autor, y, como siempre, se puede descargar gratuitamente desde la página del Departamento de Matemática de la Facultad de Ciencias Exactas y Naturales de la Universidad de Buenos Aires http://cms.dm.uba.ar/material/paenza/libro8/ .
Un muy buen libro como los que Paenza nos tiene acostumbrados. Hay un festín de problemas ingeniosos y sus respectivas soluciones
CONTRATAPA
Adrián Paenza ha demostrado que la matemática sirve para mucho más que aburrirnos en el colegio. Este nuevo libro es un mar de ideas, juegos, desafíos, estrategias, ingenio y, sobre todo, magia. ¿Qué método debería usar una encuesta para ser infalible? ¿Puede la matemática resolver un caso judicial? ¿Cómo se hace para ganar una subasta por Internet? En una reunión con amigos, ¿cómo se puede demostrar que siempre dos personas tienen la misma cantidad de amigos presentes? ¿De qué secreto nos provee la matemática para ganar a la batalla naval? ¿Cuál es la mejor forma de organizar parejas para ir a un baile? Si tiramos una moneda diez veces seguidas, ¿saldrá más veces cara o ceca? ¿Cómo descubrir la combinación de un candado? Si una escuela tiene cuatro campanas, ¿cuántos órdenes posibles hay para que suenen? Si un hombre tiene dos hijos, uno de ellos es varón y nació un martes, ¿qué probabilidad hay de que los dos sean varones? La matemática recreativa se puede aplicar para solucionar problemas cotidianos, despertar el pensamiento lateral, agilizar la mente, divertirnos y aprender.

Algo del capítulo : LA BATALLA NAVAL MEZCLADA CON PASTILLAS, ARAÑAS Y MOSCAS
LA BATALLA NAVAL
En mi paso como alumno de colegios primarios y secundarios, la variedad de juegos que estaban a nuestra disposición era muy limitada. Es decir, yo creo que en ese momento no me daba cuenta, pero ahora, viendo la cantidad de plataformas posibles, advierto que teníamos posibilidades muy restringidas. Eso sí, éramos felices igual.
De todos los entretenimientos a los que podíamos recurrir, que no fuera durante un recreo sino mientras estábamos en los bancos (hora libre, condiciones del tiempo que hacían imposible salir al patio, etc.), hubo uno que nos tenía muy ocupados: ‘la batalla naval’.
No sé si aún se sigue jugando (dudo que sea con la misma intensidad), pero para los que nunca escucharon hablar de ella hago una breve descripción: intervienen dos participantes. En una hoja cuadriculada, cada uno dibuja un cuadrado de 10 10.
Cada jugador tiene un número de ‘barcos’ (formados por ‘cuadraditos’) que distribuye en ese ‘tablero’ de 10 10. Los barcos consisten en rectángulos de 1 125, 2 1, 3 1, 4 1 y 5 1 (o también de 1 2, 1 3, 1 4 y 1 5). De esta forma, los barcos pueden ser dispuestos en forma horizontal o vertical. Además, puede que haya varios de la misma longitud, pero eso forma parte de las convenciones particulares del acuerdo con el que lleguen los dos jugadores antes de competir.
El cuadrado dibujado en la hoja cuadriculada está marcado como un mapa. Es decir, en la parte horizontal, cada columna está etiquetada por una letra. Estas letras van desde la A hasta la J, mientras que cada fi la, lleva un número que van desde el número uno hasta el diez.
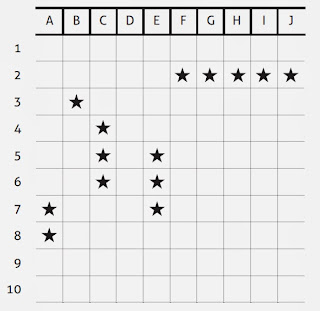
Una vez que cada uno distribuyó sus barcos, el juego empieza cuando uno de los participantes trata de identifi car alguno de los cuadraditos del rival, imaginando que allí hay un barco del oponente. Si en esa posición, digamos E4 (ver figura 1), no hay ubicado ningún barco rival, entonces éste contesta diciendo: ‘agua’. Eso indica que en esa posición no hay más que agua. En cambio, en el lugar E5 hay parte de un barquito. Por lo tanto, el jugador contesta: ‘tocado’ (si es que el disparo del rival coincide con un lugar ocupado por uno de los barcos, pero no es todo el barco) y ‘hundido’, si con ese ‘tiro’ el barco ha sido tocado en todos sus cuadraditos, como se ve en la fi gura 1 en el lugar B3.
¿Por qué estaré contando todo esto? Porque me interesa mostrar cómo la matemática interviene también en este tipo de juegos. ¿De qué manera? Fíjese si está en condiciones de pensar (y luego contestar) este problema.
Suponga que usted tiene nada más que un solo barco de 1 x 4 o de 4 x 1 y lo depositó en alguna parte del cuadrado. ¿Cuál es el mínimo número de tiros que una persona tiene que arriesgar
para poder garantizar que tocó a ese barco? Es decir, supongamos que estamos jugando usted y yo. Usted colocó su barco de 1 x 4 (o de 4 x 1) en el tablero. ¿Cuál es el mínimo número de tiros que yo tengo que hacer para garantizarme que con seguridad toqué su barco?
Naturalmente, poder conocer este resultado, permite elaborar una estrategia de cómo jugar, aunque estoy seguro de que ningún chico ni hoy ni nunca necesitó plantearse esta pregunta. ¿O sí?
¿La solución? Corré a buscarla en el libro.
Para descargar los demás libros de Adrián Paenza: